In questi giorni si è sentito spesso parlare di crescita esponenziale del numero di contagi e del fattore R0 associato al Coronavirus (parametro che ne descrive la contagiosità, ovvero quante persone un individuo, mediamente, può infettare). In questo articolo proviamo ad approfondire meglio l’andamento dei dati reali e a capire come la matematica, anche se piuttosto elementare, ci può aiutare a fare previsioni.
Al momento l’R0 del Coronavirus è stimato come maggiore di 2. Per seguire meglio il ragionamento che segue, supponiamo che R0 sia 2. Allora il numero di contagi seguirebbe la seguente successione a(n)=2^n: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048… (qualcuno avrà notato che questi numeri corrispondono alle memorie dei calcolatori elettronici. Ovviamente non è un caso, ma questa è un’altra storia).
Un andamento di questo tipo è detto esponenziale, e cresce molto velocemente. Qui propongo il suo grafico, per aiutarvi a capire quanto sia rapida una crescita di questo tipo.
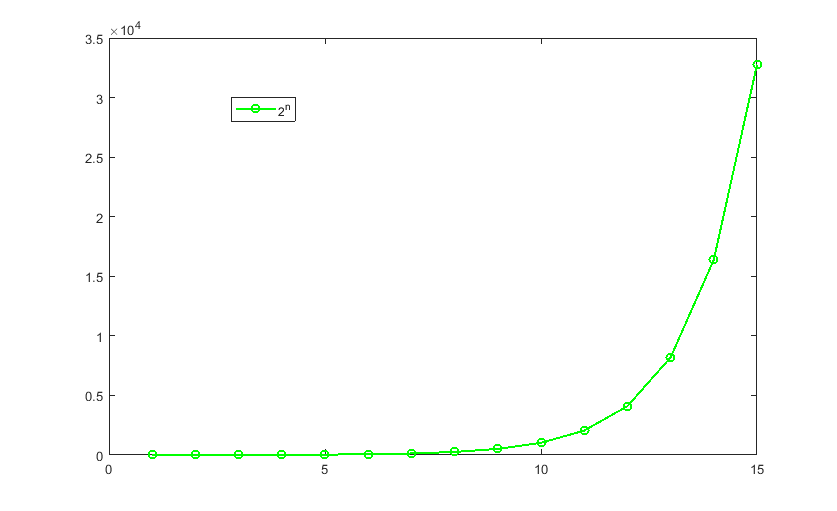
Le misure di contenimento attuate in Cina, e ora in Italia, mirano dunque a far diminuire il valore di R0. Quando questo valore sarà minore di 1, allora il contagio scomparirà gradualmente. Ad esempio, ecco il grafico di 0.8^n:
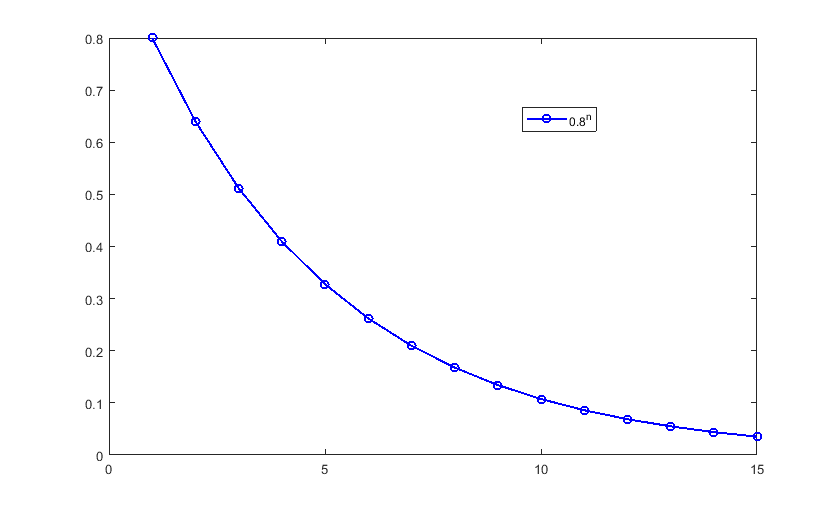
I dati a nostra disposizione stanno davvero seguendo un andamento esponenziale?
CASO CINESE
Osserviamo la crescita del numero di contagi in Cina nei primi 24 giorni dell’epidemia.
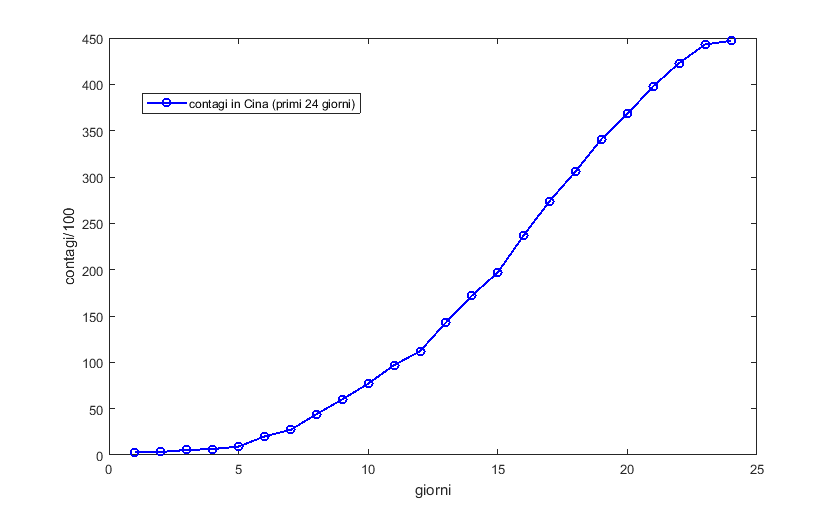
Questa curva segue un andamento esponenziale? Per capirlo ho provato ad interpolare i dati dei primi 10 giorni con una curva esponenziale (quindi del tipo a*e^(bx)) e con una curva polinomiale, per vedere quale delle due potesse approssimare meglio i dati dei giorni successivi.
Nota1: L’interpolazione è un metodo che consiste nel trovare la curva che meglio approssima i dati che abbiamo, in gergo chiamati nodi. Esistono vari tipi di interpolazione (lineare, polinomiale, spline, ecc.) e ognuna di esse ha le sue peculiarità. Solitamente l’interpolazione viene utilizzata per trovare dati “mancanti” all’interno dell’intervallo dei dati reali, mentre utilizzarla per fare previsioni all’esterno di tale intervallo è una questione molto più delicata (problemi di malcondizionamento, errori grossolani che non tengono conto dei fattori che rendono il problema complesso, ecc). Ad ogni modo, per i giorni immediatamente successivi all’intervallo considerato, come vedremo, può darci indicazioni utili.
Nota2: Tutti i grafici e i calcoli sono stati fatti utilizzando il software MATLAB.
Ecco il risultato di questa prima interpolazione. Gli asterischi corrispondono ai dati reali, la curva blu è quella data dall’interpolazione esponenziale, e la curva rossa è quella data dall’interpolazione polinomiale. Risulta evidente quanto la curva esponenziale si discosti molto dai dati reali, mentre la curva polinomiale si avvicina piuttosto bene ad essi.
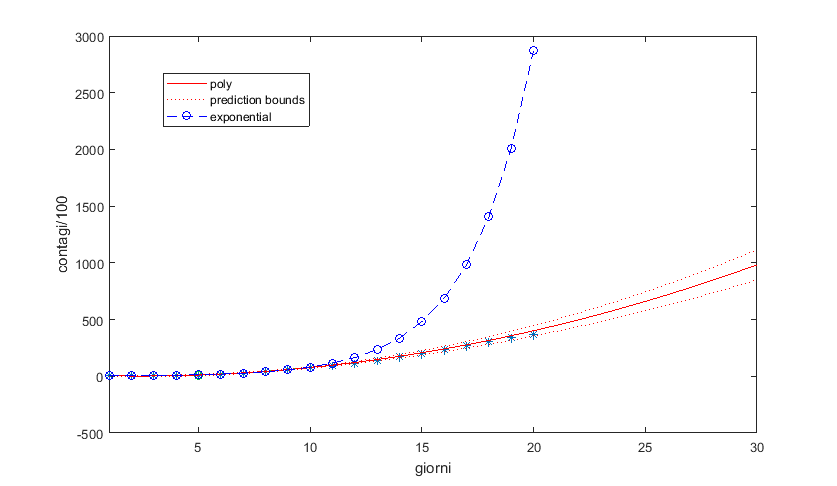
Nota3: Una curva polinomiale descrive una crescita di tipo potenza. Ad esempio, per la potenza 2, a(n)=n^2: 1, 4, 9, 16, 25, 49, 64, 81,… Per la potenza 3, a(n)=n^3: 1, 8, 27, 64, 125,…
CASO ITALIANO
Il modello di interpolazione polinomiale che avevamo costruito qualche giorno fa aveva previsto per il 2 marzo circa 1940 contagi, quindi abbiamo leggermente sottostimato il dato reale, che è 2036.
Un modello di interpolazione esponenziale, però, avrebbe previsto per il 2 marzo circa 2800 contagi, quindi il dato reale risulterebbe di gran lunga sovrastimato!
Per prevedere il numero dei contagi dei prossimi giorni preferiamo quindi attenerci, per il momento, al modello polinomiale.
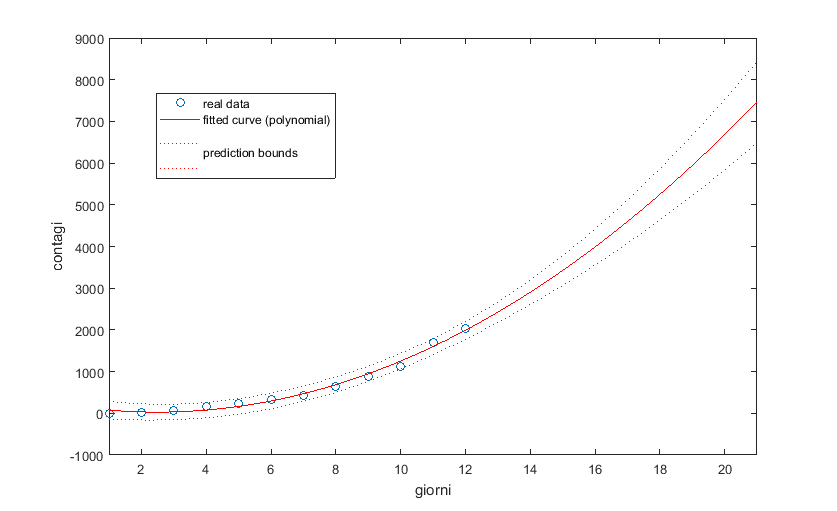
Aggiornamento 8 marzo 2020. Dove stiamo andando?
Negli ultimi 2 giorni abbiamo riscontrato un aumento significato dei casi registrati. Le nostre previsioni, che si erano adattate bene fino al 6 marzo, ora risultano troppo prudenti.
Nel grafico che segue abbiamo messo in rosso la curva dell’interpolazione precedente, in verde la curva quadratica della nuova interpolazione e in blu la curva cubica della nuova interpolazione.
Si nota subito che la cubica, pur essendo una curva polinomiale, accelera molto più velocemente della quadratica, quindi si raggiungerà prima una situazione di crisi (la retta disegnata in viola).
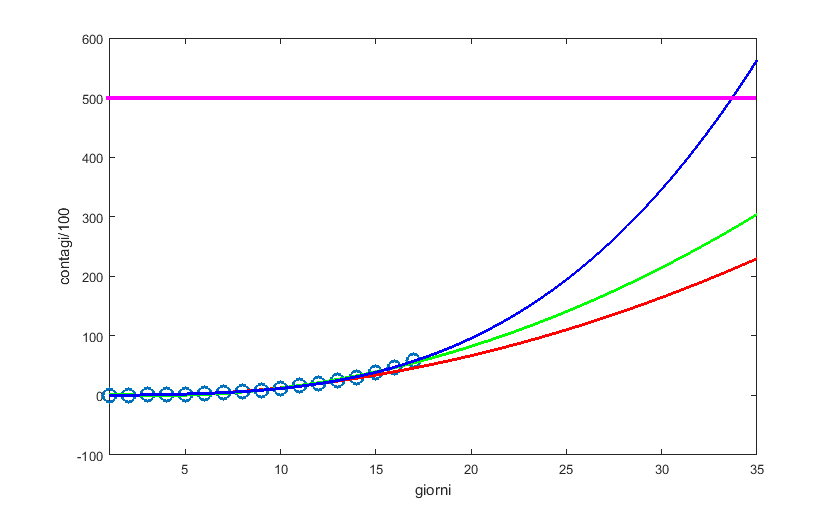
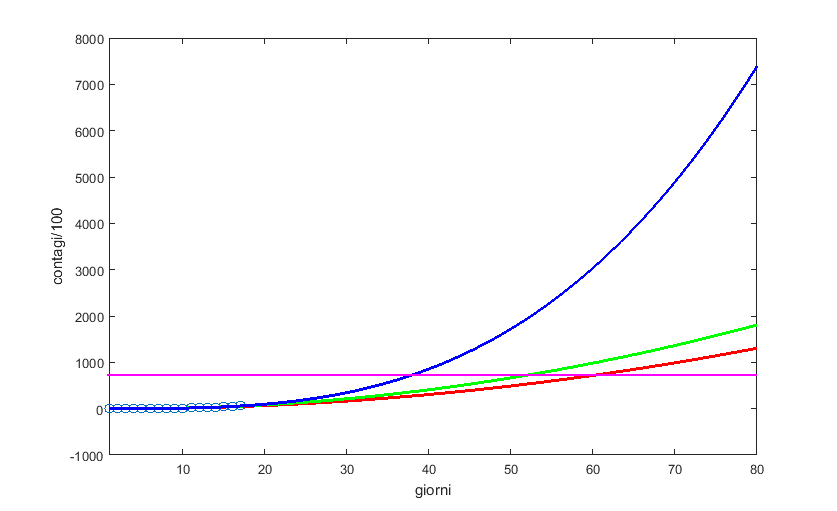
Per capirsi meglio, “ingrandiamo” il grafico aumentando il numero di giorni visibili. L’andamento di questi giorni ci suggerisce che ci stiamo avvicinando sempre più velocemente al livello di saturazione del sistema sanitario, qualsiasi esso sia. Risulta quindi urgente ritardare il raggiungimento di questo valore, tramite soprattutto le misure di contenimento che si stanno facendo sempre più stringenti. Quando si raggiungerà il picco dell’epidemia e la curva inizierà a decrescere, sarà importante trovarsi al di sotto di questo valore. Si stanno inoltre aumentando i posti letto in terapia intensiva, in modo che il valore di default incrementi e potremo guadagnare tempo.
Aggiungiamo adesso anche un fit esponenziale, in arancione, curva ancora più veloce delle precedenti. Secondo questa curva il 15 marzo dovremmo avere quasi 40000 casi.
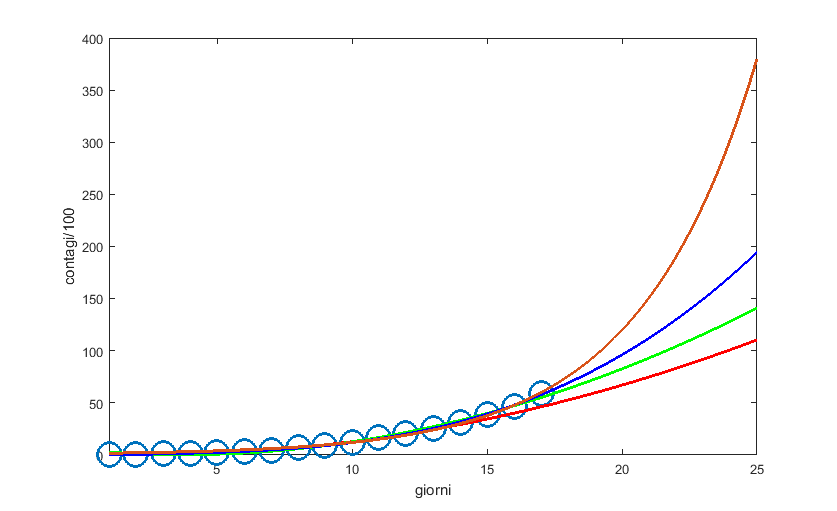
Ecco dunque la nuova previsione per i prossimi giorni.
CASO QUADRATICO
| GIORNO | CASI |
| 8/3 | 6346 |
| 9/3 | 7264 |
| 10/3 | 8244 |
| 11/3 | 9286 |
| 12/3 | 10390 |
| 13/3 | 11556 |
| 14/3 | 12785 |
| 15/3 | 14075 |
| 16/3 | 15427 |
| 17/3 | 16841 |
| 18/3 | 18318 |
| 19/3 | 19856 |
| 20/3 | 21457 |
| 21/3 | 23120 |
| 22/3 | 24844 |
| 24/3 | 26631 |
| 25/3 | 28480 |
| 26/3 | 30391 |
| 27/3 | 32364 |
| 28/3 | 34399 |
| 29/3 | 36496 |
| 30/3 | 38655 |
| 31/3 | 40877 |
CASO CUBICO
| GIORNO | CASI |
| 8/3 | 6884 |
| 9/3 | 8161 |
| 10/3 | 9594 |
| 11/3 | 11193 |
| 12/3 | 12967 |
| 13/3 | 14926 |
| 14/3 | 17079 |
| 15/3 | 19436 |
| 16/3 | 22006 |
| 17/3 | 24799 |
| 18/3 | 27823 |
| 19/3 | 31089 |
| 20/3 | 34606 |
| 21/3 | 38383 |
| 22/3 | 42429 |
| 24/3 | 46755 |
| 25/3 | 51370 |
| 26/3 | 56282 |
| 27/3 | 61503 |
| 28/3 | 67039 |
| 29/3 | 72903 |
| 30/3 | 79102 |
| 31/3 | 85646 |
Vedremo con il tempo quale sarà il modello più giusto (o meno sbagliato!).
Per un modello esponenziale, più “catastrofico” di quello qui presentato: https://statisticallearningtheory.wordpress.com/2020/03/02/previsione-della-crescita-esponenziale-dei-covid19-positivi-in-italia-lombardia-veneto-ed-e-romagna/
Per maggiori dettagli sul software e sul metodo utilizzato: https://it.mathworks.com/help/curvefit/polynomial.html
Un altro interessante articolo, più approfondito, sui modelli matematici che descrivono il propagarsi delle epidemie: http://maddmaths.simai.eu/divulgazione/focus/epidemie-matematica/
Samanta Zagani