Curva ROC (Receiver Operating Characteristic): applicazione ai test diagnostici
CURVA ROC: APPLICAZIONE AI TEST DIAGNOSTICI
La curva ROC (Receiver Operating Characteristic) è un grafico che mette in relazione la sensibilità e la specificità di un test diagnostico al variare del valore di cut-off (valore soglia).
L’analisi della curva ROC di un test diagnostico permette di valutarne l’accuratezza, di determinare il valore di cut-off più appropriato e di confrontare le performance di due, o più, diversi test.
In questo articolo richiameremo dapprima i concetti di base, essenziali per la comprensione dell’argomento, dopodiché proseguiremo introducendo nuove definizioni ed esempi.
Al termine lasceremo qualche suggerimento pratico per costruire con semplici strumenti le curve ROC e calcolarne l’AUC (Area Under the Curve).
RICHIAMO DELLE NOZIONI FONDAMENTALI
Abbiamo già diffusamente discusso di accuratezza, sensibilità e specificità dei test diagnostici nell’articolo dedicato: Sensibilità e Specificità di un Test Diagnostico.
Per praticità, riportiamo di seguito le informazioni fondamentali:
- l’obiettivo di un test è classificare correttamente un paziente (malato o sano);
- i pazienti classificati erroneamente vengono chiamati FALSI POSITIVI e FALSI NEGATIVI;
- la sensibilità di un test diagnostico è la proporzione di malati che vengono classificati in maniera corretta (SENSIBILITÀ = VERI POSITIVI/TOT MALATI = VP/(VP+FN))
- la specificità di un test diagnostico è la proporzione di sani classificati correttamente (SPECIFICITÀ = VERI NEGATIVI/TOT SANI = VN/(VN+FP))

COSTRUZIONE DI UNA CURVA ROC E SCELTA DEL CUT-OFF
In alcuni casi per determinare se un paziente rischia di contrarre una certa malattia si utilizzano test che quantificano i livelli di concentrazione di certe sostanze (ad esempio la glicemia per il diabete, il PSA per il cancro alla prostata, ecc.).
In questi casi viene scelto un valore di cut-off (valore soglia) della sostanza che permetta di discriminare nel modo più accurato possibile i malati dai sani. Ad esempio, se si volesse individuare chi è a rischio di diabete, si potrebbe scegliere un cut-off per la glicemia di 126 mg/dL (valore sopra il quale il paziente si definisce a rischio di diabete). Oppure, se si volesse individuare chi è a rischio per il cancro alla prostata, si potrebbe scegliere un cut-off di 4 ng/mL per il PSA, valore sopra il quale aumenta la probabilità che sia presente il tumore.
A questo punto è piuttosto intuitivo che, incrementando il valore di cut-off, il numero di falsi negativi aumenta, mentre diminuisce il numero di falsi positivi. Di conseguenza si ha un test altamente specifico ma poco sensibile (se scegliamo un valore di cut-off della glicemia pari a 200 mg/dL anziché 126 mg/dL è molto probabile che i pazienti che superano questo valore abbiano il diabete, quindi abbiamo pochi falsi positivi, al contempo però è molto probabile avere dei falsi negativi, cioè tutti quei pazienti che hanno un valore inferiore a 200 mg/dL e che classificheremmo come sani, ma che comunque presentano valori della glicemia molto elevati e rischiosi).
Viceversa, abbassando di cut-off, il numero di falsi positivi aumenta, mentre diminuisce il numero di falsi negativi, dunque si ha un test altamente sensibile ma poco specifico (se scegliamo un valore di cut-off della glicemia pari a 100 mg/dL anziché 126 mg/dL è molto probabile che i pazienti che non superano questo valore siano sani, quindi pochi falsi negativi, tuttavia avremmo molti falsi positivi, pazienti che superano il valore soglia ma che in realtà non presentano la malattia).
In generale, è da preferire un test sensibile quando la mancata individuazione di una malattia ha conseguenze pericolose, mentre è da preferire un test specifico quando un falso positivo può risultare dannoso (ad esempio nel caso di terapie o interventi invasivi e, chiaramente, non necessari).
La curva ROC è uno strumento molto utile per riassumere in un unico grafico le performance di un test diagnostico al variare del valore di cut-off.
Per rappresentare la curva ROC di un test si procede nel seguente modo:
- sull’asse delle ordinate (asse y) troviamo i valori di sensibilità del test, o tasso di veri postivi (TPR – True Positive Rate);
- sull’asse delle ascisse (asse x) troviamo 1 – specificità del test, o tasso di falsi positivi (FPR – False Positive Rate) (5);
- per ogni cut-off abbiamo un certo valore per la sensibilità e un certo valore per la specificità, e riportiamo sul grafico il corrispondente punto;
- unendo i vari punti si ottiene una curva con andamento “a scaletta”, la curva ROC.
ESEMPIO DI CURVA ROC
L’esempio che ora prendiamo in considerazione si trova in Pagano, Gauvreau (1) e riguarda i dati di un programma di trapianto renale in cui sono stati eseguiti omotrapianti.
Visto che l’incremento del livello di creatinina sierica è spesso associato a insufficienza renale, si è scelto di utilizzare la concentrazione di creatinina come test per individuare possibili rigetti.
I dati del programma sono riassunti nella tabella a fianco.
Ancora una volta facciamo qualche ragionamento. Se scegliamo 2,9 mg % come valore di cut-off il test ha una sensibilità di 0,303 e una specificità di 0,909, ciò significa che molti pazienti a rischio di rigetto imminente non verranno identificati (bassa sensibilità → molti falsi negativi) e che verranno quasi certamente identificati correttamente i pazienti non a rischio di rigetto (alta specificità → pochi falsi positivi).
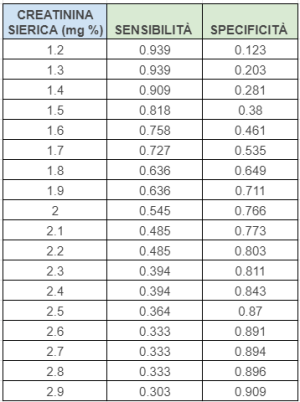
Abbassando il valore di cut-off a 1,2 mg % il test avrà una sensibilità di 0,939 e una specificità di 0,123, e risulterà difficile non identificare un paziente che presenterà il rigetto dell’organo (alta sensibilità → pochi falsi negativi) ma allo stesso tempo identificheremo erroneamente i pazienti che non presenteranno un rigetto dell’organo (bassa specificità → molti falsi positivi).
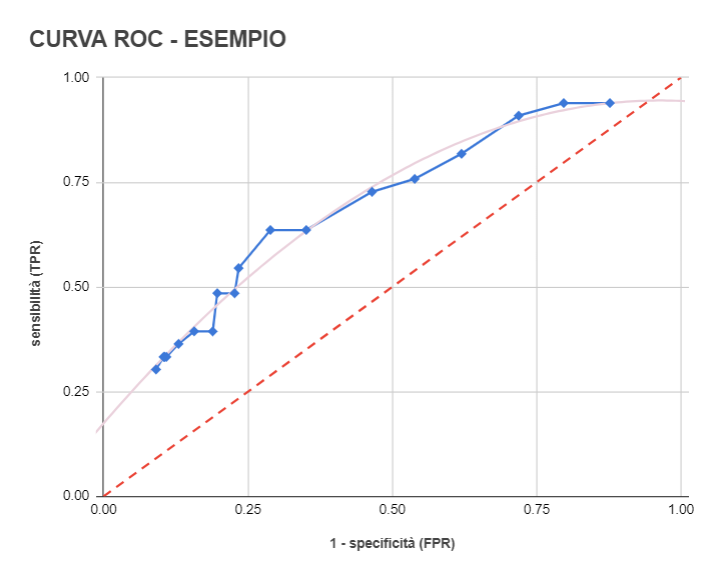
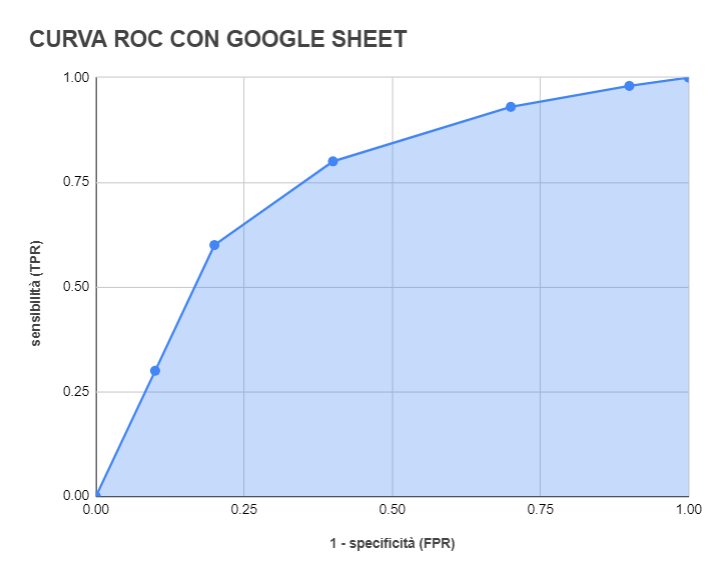
Rappresentiamo ora la curva ROC di questo test. Ovviamente, avendo a disposizione solo un numero finito di punti, il grafico che otteniamo unendo questi punti sarà una curva spezzata con andamento “a scaletta”, rappresentato in blu. Interpolando i dati possiamo ottenere invece una curva non più spezzata, che ci fornirà una stima dei dati nel caso continuo, rappresentata in violetto.
AREA UNDER THE CURVE (AUC)
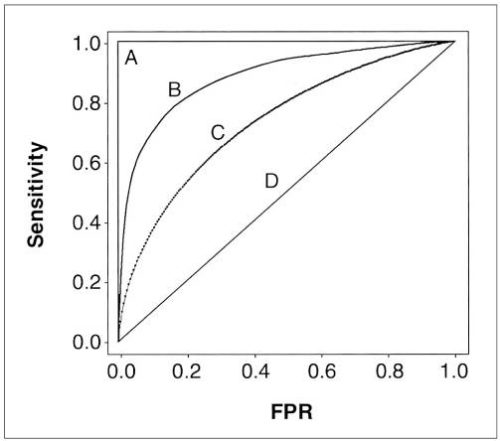
In generale un test risulta più accurato quanto più la sua curva ROC si avvicina all’angolo superiore sinistro del grafico. Per di più, il punto più vicino a tale angolo rappresenta il valore di cut-off che massimizza contemporaneamente sensibilità e specificità del test.
Detto questo, si può ora capire il perché l’area del sottografico (AUC) rappresenta una misura di quanto è accurato un test.
Se l’AUC è 0,5 il test non è informativo (la curva corrisponderebbe alla bisettrice, e il test non riuscirebbe a discriminare i malati dai sani), se invece l’AUC ha un valore compreso tra 0,5 e 1 allora il test risulta essere via via più accurato.
È chiaro dunque che un modo per mettere a confronto due test diversi sia quello di confrontare i valori delle rispettive AUC. Il test con l’AUC maggiore è, generalmente, il migliore.
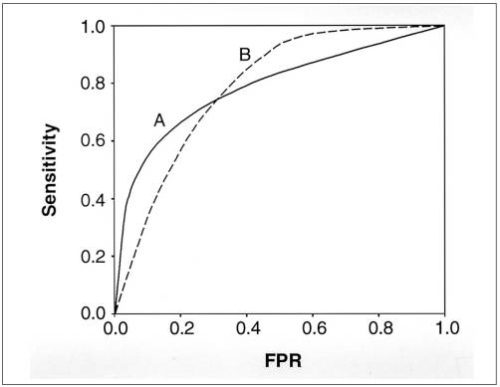
Questo metodo tuttavia ha dei limiti. Ci potrebbe essere infatti il caso di test che hanno curve ROC differenti ma hanno uguali valori dell’AUC.
In questo caso, è opportuno confrontare i due test in diversi range di intervallo. Prendendo in considerazione l’esempio rappresentato a fianco, nel range di alta sensibilità il test B è migliore del test A, mentre nel range di alta specificità il test A è migliore del test B. In questi casi un possibile metodo di confronto è quello di calcolare le aree parziali delle curve negli intervalli di interesse.
COME DISEGNARE UNA CURVA ROC CON GOOGLE SHEET (O MICROSOFT EXCEL)
Generalmente le analisi delle curve ROC e il calcolo dell’AUC vengono effettuate con software statistici dedicati, ad esempio R o SPSS, il cui utilizzo non è sempre del tutto intuitivo. Tuttavia, se non si ha la pretesa di fare analisi particolarmente avanzate, è possibile utilizzare anche strumenti gratuiti come Google Sheet (o, equivalentemente, Microsoft Excel).
Riportiamo qui un esempio.
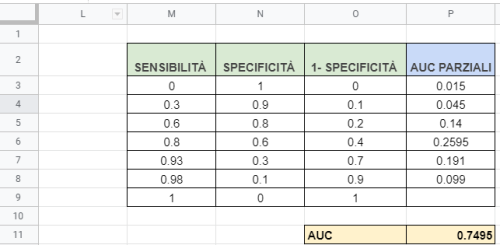
Supponiamo di avere un test con i valori di sensibilità e specificità rappresentati a fianco. Aggiungiamo una colonna e calcoliamo 1 – specificità.
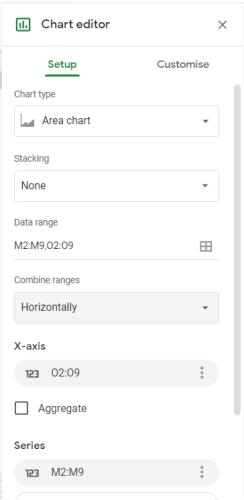
Selezioniamo le colonne M e O e inseriamo il grafico di tipo Area Chart. A questo punto potrebbe essere necessario sistemare il setup del grafico (è importante che i data-range per l’asse x e per le serie siano corretti → vedi immagine).
Per calcolare l’AUC si può usare la regola dei trapezi, che consiste nel sommare nel suddividere l’area che vogliamo trovare in tanti trapezi quanti sono i punti a nostra disposizione: nella cella P3 abbiamo inserito la formula (M3+M4)*(O4–O3)/2 che rappresenta l’area del primo trapezio (degenere). Dopodiché abbiamo copiato la formula per tutte le altre coppie di punti, tranne l’ultima, e abbiamo sommato i valori ottenuti.
Google Sheet e Microsoft Excel permettono anche di interpolare i dati usando l’opzione trend line e ottenere quindi una smooth line (metodo non del tutto ortodosso in questo caso, bisognerebbe utilizzare il maximum likelihood fit (4)).
COME DETERMINARE IL CUT-OFF OTTIMALE (INDICE DI YOUDEN)
Potrebbe essere utile, in alcuni casi, trovare il valore di cut-off che massimizzi contemporaneamente la sensibilità e la specificità del test, ovvero il cut-off ottimo.
Intuitivamente, se vogliamo massimizzare contemporaneamente sensibilità e specificità, essendo entrambe variabili dipendenti dal cut-off (c), potremmo massimizzare funzione data dalla loro somma, e poi trovare per quale valore di cut-off tale somma assume valore massimo.
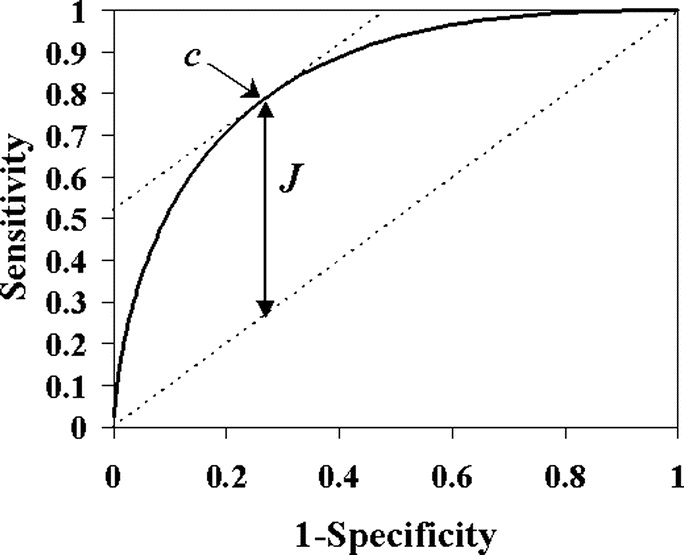
Un metodo per determinare tale cut-off è l’indice di Youden, definito come la massima distanza tra la curva ROC e la bisettrice (chance line), e si indica con J = maxc {sensibilità(c) + specificità(c) − 1}. Notiamo che massimizzare (sensibilità(c) + specificità(c) − 1) equivale a massimizzare (sensibilità(c) + specificità(c)), come affermato poc’anzi. Tuttavia la definizione data dell’indice di Youden è interessante perché è facilmente rappresentabile sul grafico (segmento verticale che indica la massima distanza tra la curva ROC e la bisettrice).
Fonti e note:
- (1) Biostatistica, Marcello Pagano, Kimberlee Gauvreau
- (2) Introductory Biostatistics, 2nd Edition, Chap T. Le, Lynn E. Eberly
- (3) Park SH, Goo JM, Jo CH. Receiver Operating Characteristic (ROC) Curve: Practical Review for Radiologists. Korean J Radiol.
- (4) Swets JA. Measuring the accuracy of diagnostic systems. Science 1998; 240: 1285-93.
- (5) Siccome sappiamo che SPECIFICITÀ = VN/(VN+FP), allora 1 – SPECIFICITÀ = 1-VN/(VN+FP)=(VN+FP-VN)/(VN+FP) = FP/(VN+FP) da cui il False Positive Rate.
- (6) Schisterman, Enrique F.; Perkins, Neil J.; Liu, Aiyi; Bondell, Howard Optimal Cut-point and Its Corresponding Youden Index to Discriminate Individuals Using Pooled Blood Samples, Epidemiology: January 2005 – Volume 16

